
 |
||||||
|
|
||||||
|
Proyectos mas complicados.
|
||||||
 |
En esta sección incluiremos experimentos y proyectos que requieren más elementos o preparativos para llevarlos a cabo y que se prestan especialmente para ser realizados por un grupo de entusiastas que se animen... |
| Midiendo el radio terrestre. | ||
| Construyamos una radio sin pilas. | ||
| Un modelo del sistema solar. | Como hacer un espectroscopio. |
 Midiendo
la aceleración de la gravedad con algunos broches para ropa, un poco de
cartón y papel de aluminio, unos cables y una computadora.
Midiendo
la aceleración de la gravedad con algunos broches para ropa, un poco de
cartón y papel de aluminio, unos cables y una computadora.
Todo lo que sube...baja, como ya sabemos (aunque con el desarrollo de la astronáutica algunas cosas suben...y se quedan allá!). Si tiramos verticalmente una piedra hacia arriba, alcanzará cierta altura (que llamaremos h) y luego comenzará a caer con velocidad creciente hasta llegar al suelo. Si la piedra tarda un tiempo t (en segundos) en caer, la física nos dice que la altura h y el tiempo t están relacionados por la fórmula:
h = (1/2) G t2 (t al cuadrado)
donde G es la llamada aceleración de la gravedad y tiene un valor de 980 cm/seg2 .
El experimento que proponemos es medir el valor de G, para lo cual dejaremos caer un objeto desde una altura h y mediremos el tiempo que tarda en llegar al suelo. Es un poco difícil medir ese tiempo "a ojo" con un cronómetro en la mano, así que nos valdremos de la grabación de un sonido que se interrumpa durante la caída. Luego mediremos la duración de esa interrupción, lo que puede hacerse fácilmente en una computadora con el programa apropiado.
Para hacer el experimento necesitaremos un generador de sonido, que puede ser un zumbador o "buzzer" comprado en un negocio de electrónica y que produzca un sonido continuo cuando conectemos sus dos patitas a una fuente de corriente continua (basta con dos pilas comunes conectadas en serie para obtener 3 voltios, lo que generalmente es suficiente). Luego deberemos armar dos partes, interconectadas como indica la figura.
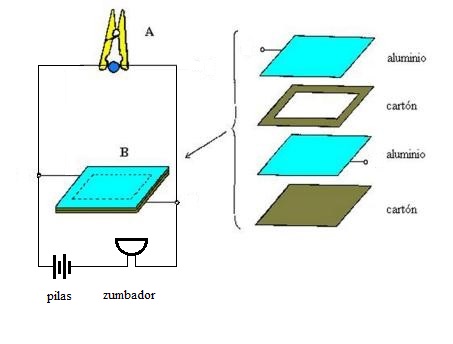 |
Parte A: un broche de ropa, de madera, con una chinche común o un clavito (no pintado) clavado en cada "patita", de manera que al sujetar con el broche una masa metálica (bolita de acero o tuerca de hierro o bronce) haya conducción eléctrica entre las chinches. Con cada chinche sujetamos el extremo bien limpio de un cable fino. Esta Parte A deberá estar ubicada a una altura de 2 o 3 metros, por lo menos. Al abrir el broche comienza a caer la masa metálica, deja de circular corriente entre las chinches, y cesa el sonido del zumbador. Parte B: debajo de la Parte A, en el suelo, ubicamos el "sensor" que indicará que la masa llegó abajo y reiniciará el sonido. Armamos esta parte como un "sandwich" de las piezas de papel de aluminio y cartón que se muestran en la figura (son de unos 20 x 20 cm), sujetas con un broche de ropa en cada vértice y cuidando que las hojas de papel de aluminio no entren en contacto. Conectamos un cable fino a cada hoja de aluminio con ayuda de un broche para papel o de una pinza "cocodrilo", de tal manera que al caer la masa sobre la hoja de arriba haga que entren en contacto las dos hojas de aluminio y la corriente pueda pasar de un cable al otro. Solo queda completar el circuito agregando las pilas y el zumbador. Puede ser conveniente agregar un interruptor entre las pilas y el zumbador (no indicado en la figura). Se debe armar todo con paciencia y cuidando que los contactos eléctricos sean buenos (limpiar bien con lija fina los extremos de los cables, las chinches y la masa metálica). |
Necesitaremos además una computadora provista de un micrófono capaz de registrar los sonidos con la "Grabadora de sonidos" que figura entre los accesorios estándar. Es conveniente ubicar el micrófono y el zumbador en cada extremo de un tubo de cartón de unos 20-30 cm de longitud, para minimizar la influencia de sonidos externos. También necesitaremos un programa para el procesamiento de sonidos, como el Audacity, que puede descargarse gratuitamente de la Internet.
Como proceder:
Con el programa Audacity funcionando, cargamos el archivo de sonido que guardamos (es posible que haya que transformarlo al formato .wav). Aparecerá en pantalla el perfil del sonido registrado, con una pequeña discontinuidad que es la información que necesitamos: cuánto tiempo estuvo inactivo el zumbador durante la caída de la masa metálica. Luego de reproducir algunas veces la grabación en el programa podremos determinar con bastante exactitud los momentos en que termina y recomienza el sonido. Ubicando el cursor en cada momento, podremos leer en la parte inferior de la pantalla el tiempo correspondiente a cada uno (en segundos y/o fracciones de segundo). La diferencia entre esos dos tiempos nos dará el tiempo t transcurrido durante la caída de la masa metálica, con una precisión de milésimas de segundo (con las centésimas estaremos conformes...).
Por otra parte, se deberá medir lo mejor posible la distancia h en centímetros existente entre la masa metálica sujeta por el broche de ropa y la hoja de aluminio del "sensor" B.
Con los datos obtenidos y sabiendo a partir de la fórmula de más arriba que G = 2 h / t2 (t al cuadrado), podremos así calcular fácilmente el valor de la aceleración de la gravedad.
Conviene repetir varias veces el experimento y promediar los valores obtenidos. No se pueden pedir valores muy exactos a un experimento sencillo como este. Si se eliminan los valores que se aparten mucho de 980 cm/seg2 (digamos más de un 15 %), el promedio obtenido no se apartará en más de un 5 % del valor esperado. Después de todo, la diversión no es medir un valor "de libro" sino preparar el experimento y hacerlo funcionar...
Observación: Hace algunos años se había propuesto este experimento utilizando una computadora como "cronómetro", para lo cual se llevaban algunos cables al conector del control de juegos. En las computadoras más modernas ese y otros conectores han sido reemplazados por los puertos USB, lo que dificulta hacer experimentos simples. Por esa razón hemos cambiado la técnica para medir el tiempo de caída de una masa, con buenos resultados.
02/17
Existen dos tipos de telescopios: refractores y reflectores. En los primeros, la imagen es formada por una lente (el objetivo) y observada con un ocular, que actua como una lupa. En los segundos, la imagen es generada por un espejo que actua como objetivo, y también es observada mediante un ocular.
Veremos como podemos fabricarnos un telescopio refractor muy sencillo, que nos permitira ver los cráteres de la Luna y también, con un poco de suerte, los satélites de Júpiter o los anillos que rodean a Saturno.
Los elementos principales que necesitaremos serán:
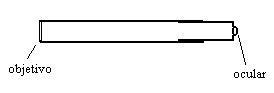 Como se ve en la Figura, debemos
fijar la lente objetivo en un extremo del tubo y además colocarle adelante un
diafragma hecho con un trozo de cartulina en el que haremos prolijamente una
abertura circular de unos 15 a 20 mm de diámetro. Si no colocamos este diafragma,
las imágenes serán muy distorsionadas. Para instalar el ocular y poder acercarlo
o alejarlo del objetivo y así enfocar la imagen, debemos fabricar un tubo de
cartón de menor diámetro, que se deslice dentro del tubo más largo; en un extremo
de ese tubo se ubicará nuestro ocular. Cuando la imagen esté en foco, el ocular
estará aproximadamente a la distancia focal del objetivo.
Como se ve en la Figura, debemos
fijar la lente objetivo en un extremo del tubo y además colocarle adelante un
diafragma hecho con un trozo de cartulina en el que haremos prolijamente una
abertura circular de unos 15 a 20 mm de diámetro. Si no colocamos este diafragma,
las imágenes serán muy distorsionadas. Para instalar el ocular y poder acercarlo
o alejarlo del objetivo y así enfocar la imagen, debemos fabricar un tubo de
cartón de menor diámetro, que se deslice dentro del tubo más largo; en un extremo
de ese tubo se ubicará nuestro ocular. Cuando la imagen esté en foco, el ocular
estará aproximadamente a la distancia focal del objetivo.
Y ya está casi listo nuestro telescopio! Casi, porque es esencial tener un buen soporte para poder observar bien. Cuanto mayor sea el aumento del telescopio, mejor deberá ser el soporte. El aumento se calcula como el cociente entre las distancias focales del objetivo (que llamaremos F) y del ocular (f); por ejemplo, si F = 100 cm y f = 2 cm, entonces Aumento = F/f = 100/2 = 50.
Volviendo al soporte, podemos sujetar el tubo del telescopio con bandas de goma a las patas de una escalera, o de una banqueta puesta al revés, etc. El tipo de soporte dependerá de las posibilidades de cada uno, pero no es una cuestión de poca importancia porque no hay nada más desalentador que una imagen de la Luna que se mueve constantemente... Y ni hablar de los planetas...
Es divertido armar un modelo a escala de nuestro sistema solar, y de paso se aprenden varias cosas. Hacer un modelo a escala significa que se deben respetar las distancias relativas a las que se mueven los planetas con respecto al Sol, así como los tamaños de los planetas, también con respecto al tamaño del Sol. Eso significa que, para comenzar, tenemos que conocer las distancias y tamaños reales, para después dividirlos por un factor de escala y llevarlos a medidas que puedan ser representadas en nuestro modelo. Esos datos iniciales que necesitamos son los siguientes:
|
Diámetro (km) |
Distancia desde el Sol (millones de km) |
|
|
Sol |
1.392.000 |
|
|
Mercurio |
4.878 |
58 |
|
Venus |
12.104 |
108 |
|
Tierra |
12.756 |
150 |
|
Marte |
6.794 |
228 |
|
Júpiter |
142.984 |
778 |
|
Saturno |
120.500 |
1.427 |
|
Urano |
51.118 |
2.871 |
|
Neptuno |
49.528 |
4.497 |
|
Plutón |
2.374 |
5.913 |
Podemos tener una primera aproximación a nuestro modelo adoptando una escala de 1 en 10.000 millones (comparar con las escalas de los mapas geográficos comunes!). Si dividimos las cantidades de la Tabla por ese factor de escala (10.000 millones o sea 1 seguido de 10 ceros, que se abrevia en matemáticas como 1010), tendremos al Sol representado por una esfera de unos 14 cm de diámetro, a Mercurio ubicado a unos 6 m del Sol y a Plutón, el planeta más lejano, a 591 m del Sol. Con esos números vamos teniendo alguna idea de las inmensas distancias que existen entre el Sol y los planetas. Y si calculamos los tamaños de los planetas usando el mismo factor, veremos que pequeños son en comparación con el Sol: nuestro querido y único planeta Tierra queda del tamaño de una cabeza de alfiler (poco menos de 1,5 mm!) mientras que el gigante Júpiter tendrá algo así como 1,5 cm de diámetro.
A partir de los datos de la Tabla es posible entonces diseñar un sistema solar en miniatura del tamaño deseado. Por ejemplo, comenzamos por definir el diámetro que tendrá el Sol en nuestro modelo y a partir de ese dato derivamos todos los otros diámetros y distancias.
Para facilitar los cálculos se ha incluído en la Página el programa SISOLAR2.EXE, que puede bajarse haciendo clic en ese nombre con el mouse. Una vez ubicado en un directorio de la computadora, bastará hacer doble-clic sobre el mismo para hacerlo funcionar (es posible que tarde algunos segundos en comenzar). Aparecerá un mensaje preguntando por el diámetro elegido para nuestro Sol en miniatura, a lo que deberá responderse con un número (en las unidades que nos convengan: milimetros, centimetros, metros...) y el programa generará una tabla con diámetros y distancias (en las mismas unidades).
Una actividad interesante puede ser armar el modelo de sistema solar en un corredor largo o en un patio, directamente en el suelo o (mejor) sobre una cinta de papel como las que se usan para las calculadoras, o simplemente sobre un rollo de papel higiénico extendido. El Sol y los planetas podrán ser representados por pelotas o bolas de adorno (de Navidad) o bolitas de plastilina o...con cualquier objeto más o menos esférico, siempre manteniendo los tamaños relativos. A trabajar y divertirse al aire libre!...
Medir el radio terrestre? No es eso una cuestión complicada y solo para especialistas? Respuesta: no, no es tan complicado. Ya en el siglo 3 A.C. un señor llamado Eratóstenes, con más ingenio que instrumentos, logró estimar la longitud del radio terrestre haciendo las mediciones que vamos a detallar.
Imaginemos a nuestro planeta Tierra, que tiene un tamaño bastante pequeño y está relativamente lejos del Sol, como mencionamos en un proyecto anterior (Un modelo del sistema solar). Los rayos del sol llegan a la superficie terrestre prácticamente paralelos. Si la Tierra fuese plana, una varilla clavada verticalmente en el suelo en Buenos Aires proyectaría la misma longitud de sombra que otra varilla igual en Tierra del Fuego o en Jujuy. Pero como la superficie de la Tierra es curva (la superficie de una esfera) las longitudes de las sombras de esas varillas no serán iguales. Midiendo esas longitudes el mismo día y conociendo la distancia entre las varillas a lo largo de un meridiano terrestre, se puede calcular la circunferencia de la Tierra y en consecuencia, su radio. Una buena descripción del experimento de Eratóstenes puede encontrarse en el libro Cosmos, de Carl Sagan (Editorial Planeta, pág. 14, 1980).
Por lo dicho, es evidente que esas mediciones deben ser hechas por dos personas o grupos de personas separados por una distancia considerable (algunos cientos de kilómetros) para obtener resultados significativos. Es, por lo tanto, una actividad ideal para ser organizada por alumnos y maestros de escuelas secundarias o de los últimos años de la escuela primaria de distintos puntos del país que se pongan de acuerdo entre sí, como es obvio. Más abajo volveremos sobre el tema.
Describimos de la manera siguiente el experimento a realizar:
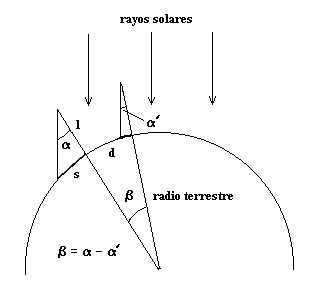 En cada lugar se debe plantar firmemente
y bien vertical un palo o varilla de 1,0 a 2,0 m de longitud, en algún patio
o lugar soleado. Se debe medir cuidadosamente la longitud de la varilla, desde
el suelo hasta su extremo. Luego, y actuando ambos grupos de experimentadores
de común acuerdo, se debe medir con todo cuidado la longitud de la sombra de
la varilla, el mismo día y en el momento en el cual la sombra esté en la
dirección Norte-Sur, anotando además la hora. A fin de eliminar discrepancias
y compensar algún problemita que aparezca (días nublados, por ejemplo...), conviene
hacer una serie de mediciones durante varios días, una por día. Veamos ahora
como interpretar y usar esas mediciones, que esquematizamos en la figura. Vemos
que el ángulo a que forma la varilla con los rayos solares es diferente para
cada lugar. Si imaginamos nuestras varillas prolongadas hasta el centro de la
Tierra, tendremos que el ángulo b que
forman esas prolongaciones es igual a la diferencia entre los ángulos a en cada lugar: b = a - a '. Conociendo ese ángulo b por nuestras mediciones y la distancia d
entre las varillas con la ayuda de un mapa, hacemos el siguiente razonamiento:
si a un ángulo b corresponde una distancia
d, a un ángulo de 360º (una vuelta completa) corresponderá una longitud
igual a la circunferencia terrestre (regla de tres!). Conociendo este último
valor, calculamos el radio terrestre.
En cada lugar se debe plantar firmemente
y bien vertical un palo o varilla de 1,0 a 2,0 m de longitud, en algún patio
o lugar soleado. Se debe medir cuidadosamente la longitud de la varilla, desde
el suelo hasta su extremo. Luego, y actuando ambos grupos de experimentadores
de común acuerdo, se debe medir con todo cuidado la longitud de la sombra de
la varilla, el mismo día y en el momento en el cual la sombra esté en la
dirección Norte-Sur, anotando además la hora. A fin de eliminar discrepancias
y compensar algún problemita que aparezca (días nublados, por ejemplo...), conviene
hacer una serie de mediciones durante varios días, una por día. Veamos ahora
como interpretar y usar esas mediciones, que esquematizamos en la figura. Vemos
que el ángulo a que forma la varilla con los rayos solares es diferente para
cada lugar. Si imaginamos nuestras varillas prolongadas hasta el centro de la
Tierra, tendremos que el ángulo b que
forman esas prolongaciones es igual a la diferencia entre los ángulos a en cada lugar: b = a - a '. Conociendo ese ángulo b por nuestras mediciones y la distancia d
entre las varillas con la ayuda de un mapa, hacemos el siguiente razonamiento:
si a un ángulo b corresponde una distancia
d, a un ángulo de 360º (una vuelta completa) corresponderá una longitud
igual a la circunferencia terrestre (regla de tres!). Conociendo este último
valor, calculamos el radio terrestre.
 Volvamos ahora al experimento. Ya
tenemos nuestros valores de longitud de varilla l y longitud de sombra
s. Cómo se calcula el ángulo a ? Se cumple que tg a
= s / l donde tg o tangente es una función trigonométrica, que
aparece siempre en las calculadoras de mano de las llamadas científicas. Entonces,
conociendo el valor del cociente s / l, que es igual a la tangente
de ese ángulo, con la calculadora obtenemos el valor de a , el ángulo que nos interesa, usando la función
inversa (arctg).
Volvamos ahora al experimento. Ya
tenemos nuestros valores de longitud de varilla l y longitud de sombra
s. Cómo se calcula el ángulo a ? Se cumple que tg a
= s / l donde tg o tangente es una función trigonométrica, que
aparece siempre en las calculadoras de mano de las llamadas científicas. Entonces,
conociendo el valor del cociente s / l, que es igual a la tangente
de ese ángulo, con la calculadora obtenemos el valor de a , el ángulo que nos interesa, usando la función
inversa (arctg).
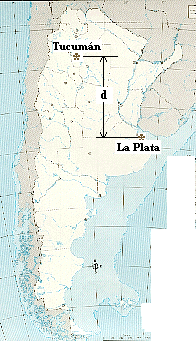
Ahora debemos obtener d, la distancia entre las localidades en las que se realizaron las mediciones. Recurrimos a un buen mapa y medimos cuidadosamente y lo mejor que se pueda la distancia entre las localidades pero sobre un meridiano (la distancia vertical entre los dos lugares) como se muestra en la figura. Usando la escala del mapa pasamos esa medida a kilómetros.
Y ya tenemos todos los datos necesarios para calcular el radio terrestre. Para poner a prueba este experimento, hemos hecho una serie de mediciones en las ciudades de Tucumán y La Plata, que pueden tomarse como ejemplo. Estos son los resultados para un día determinado:
|
Lugar |
Día |
Hora |
Long. varilla (l) |
Long. sombra (s) |
s / l |
a |
|
La Plata |
20 Octubre |
12:48 |
166,0 cm. |
76,5 cm. |
0,4608 |
24,75º |
|
Tucumán |
20 Octubre |
13:22 |
173,1 cm. |
51,6 cm. |
0,2981 |
16,60º |
Y se deduce:
b = a - a ' = 24,75 - 16,60 = 8,15º
Del mapa (figura) se obtiene d = 900 km.
y entonces: circunferencia terrestre c = (900 km. x 360º) / 8,15º = 39755 km.
y siendo la relación entre la circunferencia y el radio igual a c = 2 p r, se obtiene r = 6327 km, en excelente acuerdo con el valor real de 6378 km. para el radio de nuestro planeta!
Se habrán dado cuenta que en la Tabla figura la hora a la que se hicieron las medidas, cuando la sombra estaba en la dirección Norte-Sur. Cada grupo puede proponer algún uso para ese dato extra!
La Página de la Ciencia se ofrece como medio de comunicación entre los grupos que quieran llevar a cabo este experimento tan interesante (y en qué escala!). Basta con enviar un mensaje a la dirección de e-mail de la Página (pagciencia@quimica.unlp.edu.ar) identificándose y dando la localización geográfica precisa (nombre de la localidad, provincia, país). Las correspondientes direcciones de e-mail serán comunicadas a todos los interesados o aparecerán en esta Página, para que cada grupo se comunique con alguno (o algunos) de los otros grupos y se pongan de acuerdo para realizar las mediciones e intercambiar resultados. Y de paso, será una magnífica oportunidad para establecer contactos con otras gentes de nuestra enorme geografía. Que se diviertan y aprendan mucho!
Se agradece la colaboración de Ana C. Gómez Marigliano, de la Universidad Nacional de Tucumán, en las mediciones efectuadas.
Como parte de las celebraciones por el "2005, Año Mundial de la Física" se realizó esta experiencia, tal como está descripta en esta Página, en diversas escuelas de las ciudades de Rosario, Bariloche, Caleta Olivia, La Plata y Asunción del Paraguay. El Prof. R. Welti, de Rosario (Santa Fe), coordinó los distintos grupos que realizaron sus mediciones a fines de setiembre de ese año.
 Construyamos
una radio sin pilas.
Construyamos
una radio sin pilas.
Es bastante sencillo construir una radio como las que utilizaban nuestros abuelos (o bisabuelos!) a principios del siglo XX. Aquellas eran las "radios a galena", que utilizaban un trocito de galena (que es un mineral de azufre y plomo) para detectar las señales. Claro que tenían el inconveniente de ser radios para uno solo, ya que había que escuchar con auriculares. Además, las estaciones tenían que estar cerca, digamos a una distancia no mayor de 40 Km.
Las partes principales que necesitaremos para armar nuestra radio serán: una bobina, un diodo detector, los auriculares, la antena y la conexión a tierra. Vayamos por partes:
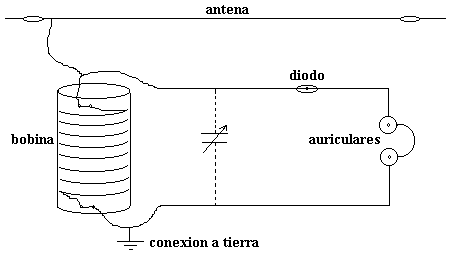 |
Teniendo cuidado de limpiar muy bien los cables que vamos a unir con lija fina o con ayuda de un cuchillo, cortaplumas, etc., armamos nuestro receptor sobre una tablita como se indica en la figura. Si todo anduvo bien y existe alguna estación de AM en las cercanías (no, con las estaciones de FM no funciona...) y la antena es suficiente, deberíamos escuchar algo en los auriculares. Es posible que en las ciudades grandes se escuchen dos o más estaciones superpuestas. Para separarlas y sintonizar nuestro receptor, deberá agregarse un condensador variable, conectado donde aparecen las líneas cortadas en la figura. Para conseguir este condensador, habrá que recurrir al electrónico del barrio y/o desarmar alguna radio vieja que ya no funcione. |
La Página de la Ciencia. 02/17